Introduction to Neutrino Oscillation
Neutrino oscillation, now a well-understood phenomenon, indicates that neutrinos have mass, and their flavor eigenstates are different from their mass eigenstates. Neutrino oscillations provide the first evidence of physics be- yond the Standard Model of the elementary particles. Over eight decades, our picture of neutrino physics has been revolutionized, but some fundamental questions still remain unanswered. Neutrino oscillations spring from a quantum mechanical mixing between the mass and flavor eigenstates of neutrinos. Neutrinos, which are observed in the experiments, are created with other fermions through weak nuclear force, which does not change the flavor of the particle. The νe, νμ and ντ are labeled as the flavor eigenstates of neutrinos (generalized as να). The only way flavor eigenstates of neutrinos can be constructed to be invariant under weak nuclear force is a mixture of exactly the right portion of the three flavor-mixed eigenstates ν1, ν2 and ν3. The flavor eigenstates can be derived from the mass eigenstates with a leptonic mixing matrix Uαi, so-called PMNS mixing matrix. The probability of observing a neutrino of flavor β (νβ) at time t (equivalent to distance L) from a neutrino of original flavor α (να) is then given by:
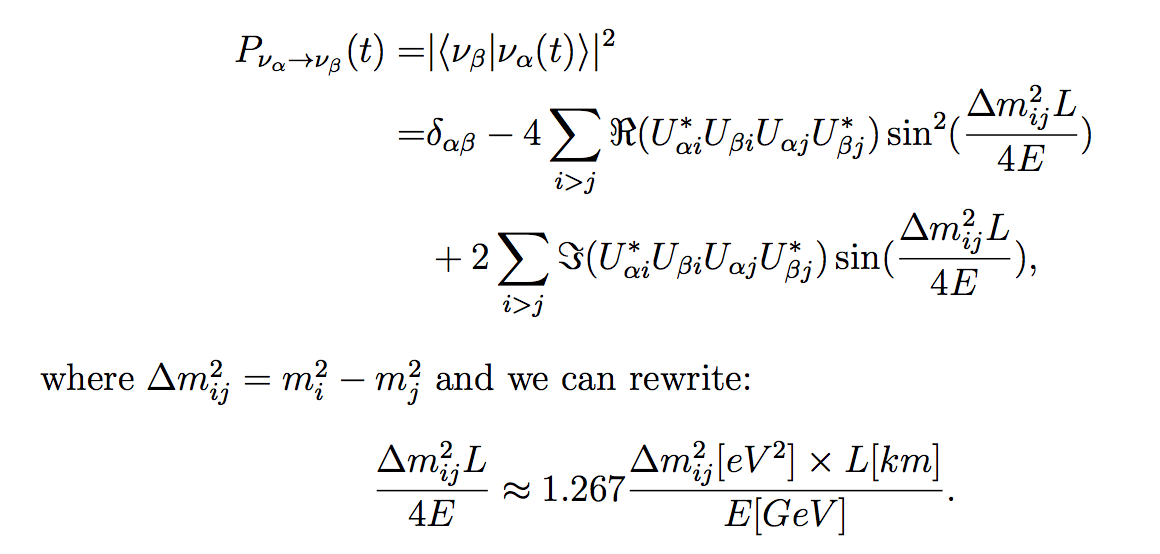
General form of oscillation probability
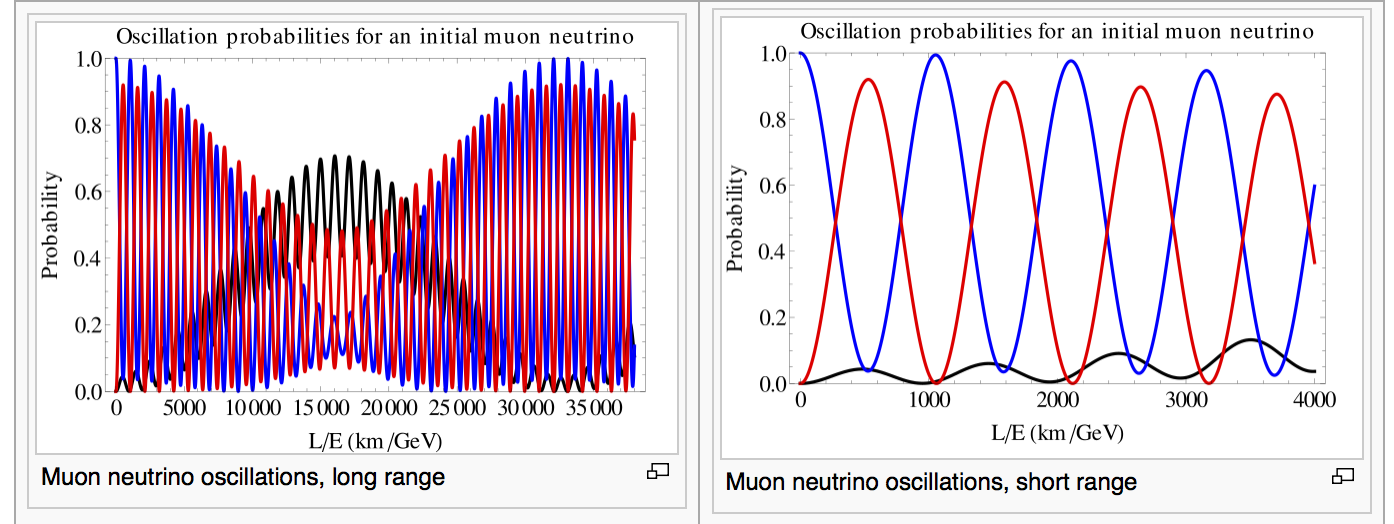
Oscillation probabilities from νμ to νe (black), νμ (blue) and ντ (red). Credit: wikipedia
The above graph is examples of oscillation probability from νμ to νe (black), νμ (blue) and ντ (red) an initial muon (flavor) neutrino to other flavors (electron, muon, tau) neutrinos. The oscillation probabilities depend on the baseline (distance btw neutrino production source and neutrino detector) and neutrino energy.
How can we measure neutrino oscillations?
To measure neutrino oscillations, at first we need a source of neutrino in which neutrino flavor components (number of electron neutrinos, muon neutrino, tau neutrinos) are well-understood. It can be from nature (the sun, atmospheric, supernova, etc..) or man-made source (accelerator, accelerator, etc..). In principle, one large detector, which is placed at the location such that the considering oscillation probability is almost maximum, is enough. However, an additional detector placed near the neutrino source (so-called near detector, and the previous one is so-called far detector) is often necessary to understand the neutrino flux before neutrino oscillates.This is so-called two-detector baseline paradigm. In current long-baseline neutrino experiments, T2K and NOvA uses far detector at 295km and 810km away from the neutrino source respectively. These optimal baselines depends mainly on energy of neutrino flux and target of the neutrino physics. There are two conventional ways to measure neutrino oscillation: disappearance and appearance.
- Disappearance: to see how much neutrino of original flavor α (να) reduces after traveling a defined distance. For example, you have a beam of νμ and you predict that you will see Nνμ neutrino events of classified νμ in detector. However what you observed is Mνμ events, which is smaller the predicted Nνμ. In that case, we say, νμ is deficit or νμ is disappeared.
- Appearance: to see a how much neutrino of new flavor β (νβ) is appeared from a defined neutrino να flux (𝛽≠α). For example, you have a beam of νμ and you predict that you will see Nνe event of νe in your detector (can be from intrinsic beam- there is no beam with 100% νμ, or from misclassified event) if neutrino oscillation is not existed. However you observe Mνμ events of classified νe event, which is larger the predicted Nνe. In this case, we say νe is appeared.
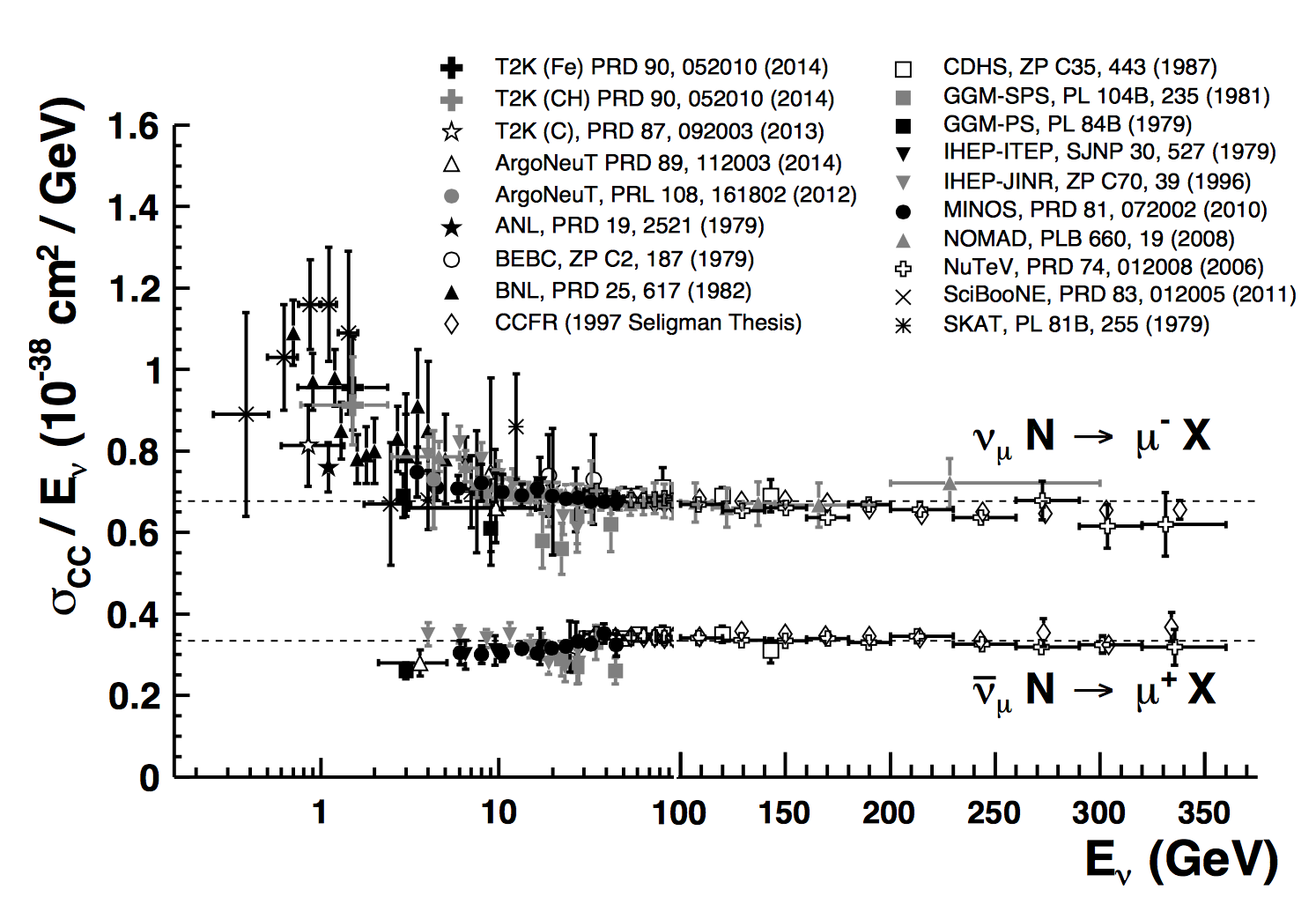
It is reminded that the neutrino oscillation probability depends on its energy. Thus for precise measurement, it is necessary to reconstruct energy for each neutrino event and present disappearance or appearance as a function of energy. These pattern then is fitted with the oscillation probability formulas to extract the neutrino oscillation parameters.
Present neutrino oscillation landscape
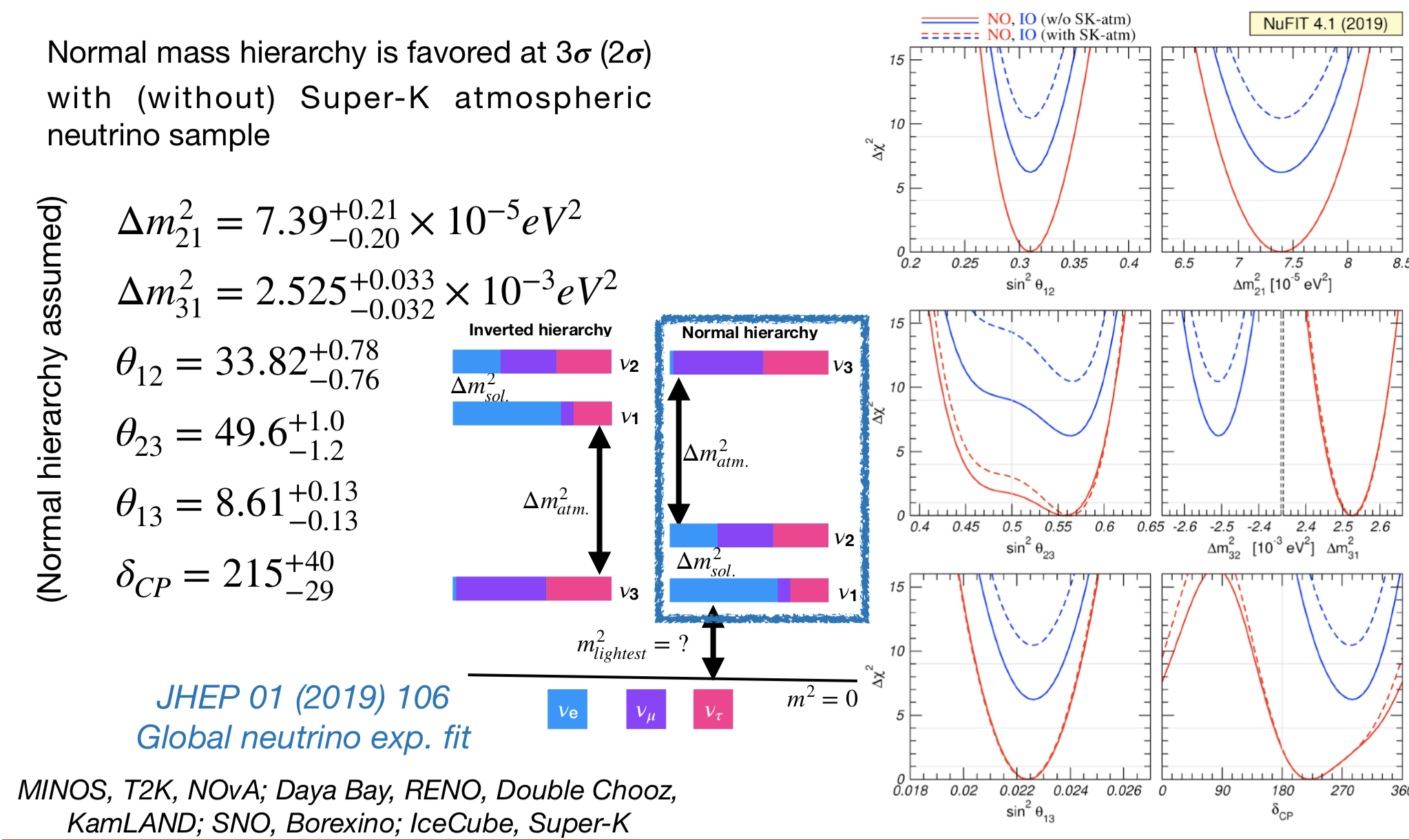
What we know and what we don’t know, from S. Cao’s slide at "3 neutrinos and beyond" 2019
Learn more about Neutrinos
-
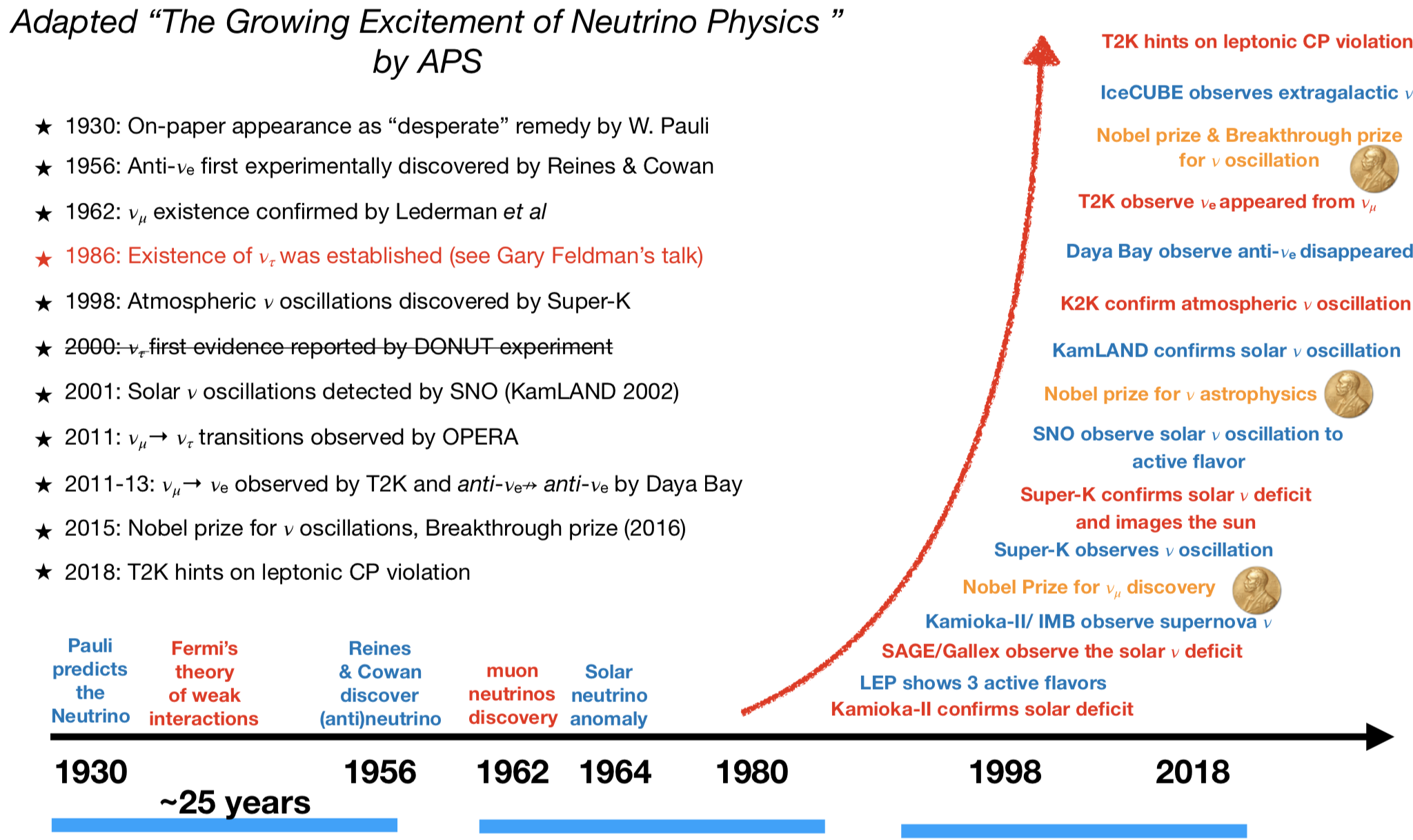
Introduction to neutrino
brief history, what we know/don't know...
-

How can we see neutrino?
Assume neutrinos hit on the material inside detector, what is next? ...
-
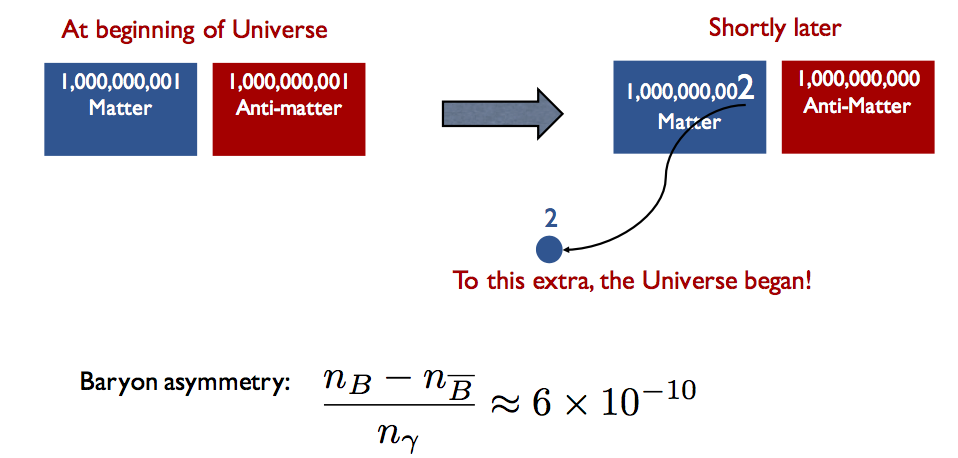
Search for CP violation
Can neutrino be our ultimate mother, a reason for our matter-dominated Universe...